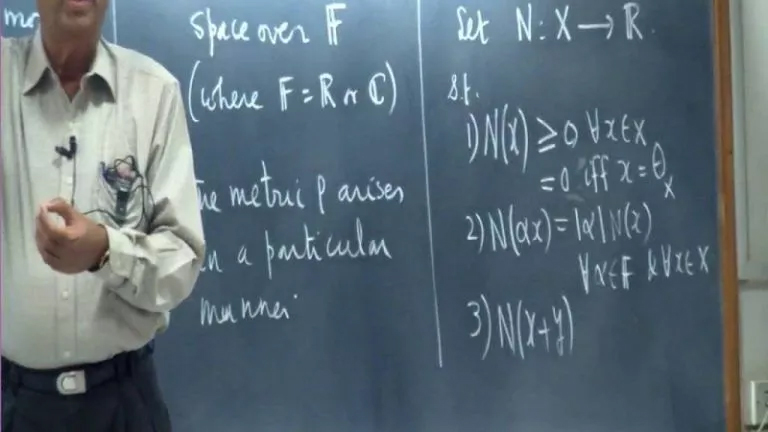Functional Analysis Homework Help

Functional Analysis Assignment Help

Functional Analysis is an advanced branch of mathematics that deals with classical analysis and its applications, including vector spaces, linear operators, topology, Fourier transforms, and convexity. Our Functional Analysis Homework Help provides reliable support for college students, offering expert guidance to simplify complex topics. With our tailored assistance, you can enhance your academic performance and gain a deeper understanding of Functional Analysis.

Functional Analysis Tutors

Functional Analysis has numerous practical applications in applied science, mathematics, and fields that require a deep understanding of function spaces and their structures. Our online Functional Analysis Tutors provide personalized, expert guidance tailored to your academic needs. Whether you're tackling challenging assignments or understanding complex theories, our tutors are available to help you master Functional Analysis concepts confidently. Get the Functional Analysis Homework Help you need from experienced professionals, available anytime, anywhere.

Functional Analysis Homework Help and Assignment Help

Functional Analysis is a challenging branch of mathematics that many students find difficult to understand and apply. As such, most students seek expert help to tackle assignments and grasp complex concepts. For those students, we offer Functional Analysis Homework Help and Functional Analysis Assignment Help online through our platform, onlinecollegehomeworkhelp.com, where experienced tutors are ready to assist with challenging topics in Functional Analysis.

Upload Your Homework/Assignments to Our Online Tutoring Centre

If you're struggling with assignments and practical analysis projects, expert assistance is just a click away. At onlinecollegehomeworkhelp.com, you can upload your homework or assignments for expert guidance. Our Functional Analysis tutors are ready to assist you in understanding the material and improving your problem-solving skills. Take advantage of this resource to overcome challenges in Functional Analysis.

Get Live Online Tutoring for Functional Analysis

Individual tutoring sessions are more effective than group classes for ensuring that students fully understand the material. Our Functional Analysis Tutoring Help offers personalized, live online tutoring sessions with expert tutors. These interactive sessions help clear any doubts and answer questions regarding Functional Analysis topics. You can also ask questions about resolved queries without any additional charges. Get the help you need to master Functional Analysis today!

Benefits of Mastering Functional Analysis

Enhanced Problem-Solving Skills: Mastering Functional Analysis equips you with powerful tools to solve complex mathematical problems. Concepts like normed spaces, Banach spaces, and Hilbert spaces enable you to approach challenging problems in mathematics and science effectively.

Advanced Research Opportunities: Proficiency in Functional Analysis is fundamental for advanced research in pure and applied mathematics. Mastery of this subject opens doors to cutting-edge topics such as spectral theory, operator theory, and functional equations, making you a valuable asset in academic and research settings.

Improved Computational Techniques: Functional Analysis provides essential methods for dealing with infinite-dimensional spaces and operators, crucial in fields like engineering, physics, and computer science. Expertise in this area enhances your ability to apply algorithms for complex simulations and analyses.

Stronger Theoretical Foundation: A solid grasp of Functional Analysis strengthens your understanding of other advanced mathematical disciplines, including differential equations, optimization theory, and quantum mechanics. This foundational knowledge is invaluable in both academic and professional settings.

Increased Career Opportunities: Expertise in Functional Analysis is highly regarded in academia, research, and various industries. Fields such as data science, signal processing, and systems engineering require a deep understanding of Functional Analysis principles, providing a competitive edge in the job market.

By mastering Functional Analysis, you not only advance your mathematical knowledge but also unlock numerous opportunities for personal and professional growth. Whether you aim for a career in mathematics, engineering, or related fields, a strong understanding of Functional Analysis can be a significant asset to your academic and professional development.

Receive Online Functional Analysis Help You Need Today!

Our mission is to provide students with a thorough understanding of Functional Analysis. We help clarify doubts, enhance knowledge, and improve grades by connecting students with expert tutors in the field. Our Functional Analysis homework help experts are available online 24/7 to assist with assignments and homework. Whether you're facing challenges with specific topics or need help completing your assignments, our tutors are ready to help you succeed.

Branches of Functional Analysis where we provide Homework & Assignment Help

Functional analysis is a broad field of mathematics with various sub-branches that focus on different aspects of mathematical spaces, operators, and their interactions. Below are some of the key branches of functional analysis:

• Normed Vector Spaces: This branch studies vector spaces equipped with a norm, a function that assigns a positive real number to each vector, which measures its "size" or "length." Key concepts include Banach spaces, which are complete normed vector spaces.
• Banach Spaces: A Banach space is a complete normed vector space. The study of Banach spaces focuses on properties like convergence, completeness, and the interaction of various types of norms. Banach's fixed-point theorem is a famous result in this branch.
• Hilbert Spaces: Hilbert spaces are a special case of Banach spaces where the norm comes from an inner product. This branch is essential for quantum mechanics, signal processing, and Fourier analysis, as it deals with infinite-dimensional spaces that generalize Euclidean space.
• Linear Operators: This branch examines the properties of linear operators, which are functions that map elements of a vector space to other elements in the same or another space. It includes the study of bounded, unbounded, and compact operators, as well as spectral theory.
• Spectral Theory: Spectral theory studies the spectrum (set of eigenvalues) of operators, especially in the context of Hilbert and Banach spaces. It is critical for understanding quantum mechanics, where operators represent observable quantities like energy and momentum.
• Functional Spaces: This branch focuses on the study of spaces of functions, such as \( L^p \) spaces, Sobolev spaces, and spaces of continuous functions. These are crucial in solving differential equations and understanding the regularity of solutions.
• Operator Theory: Operator theory studies the algebraic and topological properties of linear operators, particularly the actions of operators on Banach and Hilbert spaces. Topics include boundedness, compactness, and the theory of operator algebras.
• Topological Vector Spaces: This area deals with vector spaces endowed with a topology, which allows the study of continuity, convergence, and compactness in vector spaces. The theory of topological vector spaces generalizes many concepts of finite-dimensional spaces to infinite dimensions.
• C*-Algebras and von Neumann Algebras: These algebras are studied in the context of operator theory and functional analysis, particularly in quantum mechanics and functional analysis. C*-algebras arise in the study of continuous symmetries, while von Neumann algebras are central to quantum theory and statistical mechanics.
• Compact Operators: Compact operators are a class of operators that behave similarly to matrices in finite dimensions. This branch deals with operators that can be approximated by finite-rank operators and is important in solving integral equations.
• Convex Analysis: Convex analysis studies convex sets and convex functions, which play a crucial role in optimization problems. Functional analysis provides the tools to analyze these convex structures, particularly in infinite-dimensional spaces.
• Fixed-Point Theory: This sub-branch studies the existence and properties of fixed points of functions, such as those described by Banach's fixed-point theorem. Fixed-point theorems have applications in various fields, including nonlinear analysis and differential equations.
• Nonlinear Functional Analysis: Unlike traditional functional analysis, which mainly deals with linear spaces and operators, nonlinear functional analysis investigates spaces and operators where linearity does not hold. This area has applications in differential inclusions, variational problems, and optimization.

Each of these branches plays an integral role in advancing the understanding of mathematical structures and solving practical problems in fields such as physics, engineering, and economics.

Frequently Asked Questions About Functional Analysis Homework Help